6.3.4. Множественное наследование

В то определение понятия наследования, которое было дано в работах Квиллиана, концепция фреймов внесла определенные коррективы. В настоящее время является общепризнанным, что некоторый фрейм может наследовать информацию от множества предшественников в системе фреймов. В результате граф, представляющий связи между фреймами, стал больше походить на решетку, чем на дерево, поскольку каждый узел не обязательно имеет единственного предшественника. Очень часто система строится таким образом, что некоторые фреймы имеют несколько предшественников, хотя в подавляющем большинстве структур сохраняется единственность корня. Пример такой структуры представлен на рис. 6.7.

Новый узел Правильный многоугольник "не вписывается" в прежнюю классификацию, в которой за основу бралось количество сторон. Этот фрейм вводит в систему новый атрибут— "правильность" контура фигуры. Таким образом, появляется возможность передать таким фреймам, как Квадрат и Равносторонний треугольник, некоторые свойства, характерные именно для равносторонних фигур, использовав для этого механизм множественного наследования. Например, все равносторонние многоугольники имеют равные значения внутренних углов, и лучше всего хранить информацию об этом свойстве именно во фрейме Правильный многоугольник, как это следует из принципа когнитивной экономии.

Такая организация связей между фреймами не влечет за собой никаких проблем только до тех пор, пока информация, поступающая от различных источников наследования, не становится противоречивой. Но рассмотрим пример, представленный на рис. 6.8. (Он часто используется в специальной литературе и даже получил имя собственное — "Алмаз Никсона", по причинам, которые станут ясны далее.)

Положим, мы договорились считать по умолчанию, что квакеры — это пацифисты, т.е. в слоте пацифизм фрейма квакер "прописано" значение истина, и что республиканцы пацифистами не являются, т.е. в слоте пацифизм фрейма республиканец "прописано" значение ложь. Все это означает, что при отсутствии более полной информации о каком-либо конкретном республиканце или квакере предполагается, что он именно так относится к идеям пацифизма.

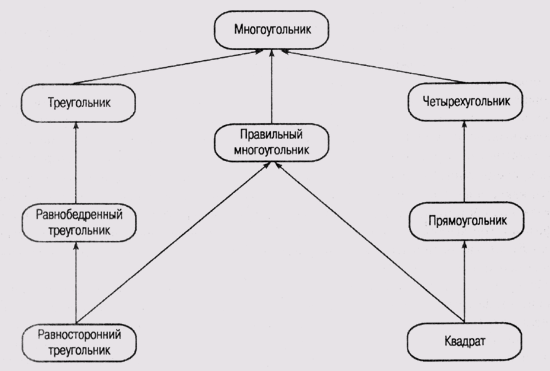
Рис. 6.7. Гетерархическое представление множества геометрических фигур

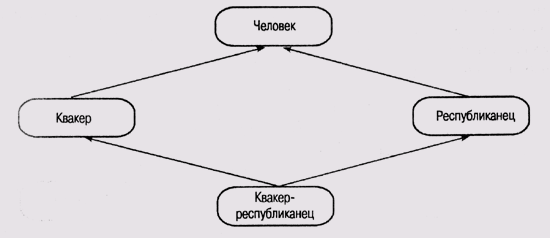
Рис. 6.8. Конфликт при множественном наследовании свойств

Но что в таком случае можно сказать о квакере, который является сторонником Республиканской партии? А ведь именно в такой роли выступал бывший Президент США Ричард Никсон. Является ли он пацифистом или нет? Иными словами, откуда должен унаследовать квакер-республиканец значение слота пацифизм, если считать, что мы не располагаем никакой дополнительной уточняющей информацией?

Поскольку значения, предлагаемые по умолчанию, конфликтуют друг с другом, мы, используя только ранее введенную информацию, не можем ничего сказать о пацифизме Ричарда Никсона. В такой ситуации некоторые системы, использующие механизм наследования, отказываются давать однозначное заключение. Системы с таким поведением получили наименование скептических (см., например, [Horty et al, 1987]). Другие, обнаружив подобный конфликт, выносят заключение наудачу. За ними закрепилось определение доверчивые (см., например, [Touretzky, 1986]).

Трудно отдать предпочтение какой-либо из этих стратегий. Но в любом случае лучше заранее подумать о том, как избежать подобных конфликтов при внедрении систем фреймов. Например, можно оспорить мнение, что миролюбивый республиканец — явление более редкое, чем квакер, поддерживающий акции с применением силы, и либо установить определенный порядок анализа наследования от различных предшественников, либо не использовать в данном случае механизм наследственности и принудительно установить значение истина для слота пацифизм во фрейме квакер-республиканец. Есть и альтернативный вариант— подключить к слоту пацифизм во фрейме квакер-республиканец специальный демон по требованию, использующий "для устранения неоднозначности какие-либо "посторонние" знания, которыми мы не располагаем на стадии конструирования системы фреймов. Так, квакер-республиканец может не следовать идеям пацифизма в год выборов в соответствии с общей политикой своей партии, но в обычное время будет рассматриваться как пацифист, полагая, что квакерское воспитание пересиливает партийную дисциплину.

Следует отметить, что анализ сетей с наследованием оказывается проще, чем анализ систем фреймов, поскольку узлы в сети не нуждаются в слотах или подключенных процедурах. Неоднозначность в сети устанавливается путем анализа ее топологии. Для того чтобы в сети потенциально могла появиться неоднозначность, о которой идет речь, необходимо, чтобы набор узлов {А, В, С, ...} образовал ациклический граф со связями двух типов: положительные связи, которые означают, что А является элементом В, и отрицательные связи, которые означают, что А не является элементом В. Тогда мы сможем представить проблему выяснения глубины пацифистских взглядов Р. Никсона в виде сети рис. 6.9. Здесь пацифист — это узел со своими собственными правами, и отрицательный характер связи между ним и узлом республиканец показан засечкой на линии связи.

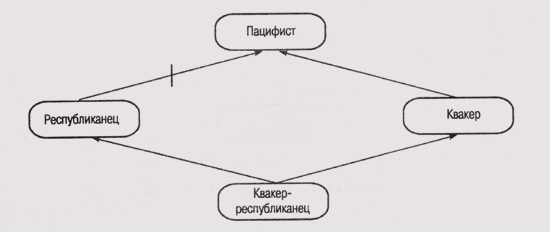
Рис. 6.9. Представление "проблемы Никсона" в виде сети с наследованием

Из изложенного ясно, что в гетерархической системе потенциальные возможности для образования самых разнообразных взаимосвязей гораздо шире, чем в системе с жесткой иерархической структурой. Узлы более высоких уровней могут иметь общих наследников на более низких уровнях, что является признаком существования непрямых отношений между такими узлами. Например, имеются определенные отношения между узлами, представляющими равносторонний треугольник и квадрат в рассмотренном выше примере. В системе фреймов значение некоторого слота также может быть указателем на определенный фрейм (или фреймы), что порождает еще одно измерение в структуре системы (см. об этом в описании системы CENTAUR в главе 13).