19.4.2. Использование систем отслеживания истинности предположений для диагностирования на основе моделей

Выше, в главах 11 и 12, были рассмотрены экспертные диагностические системы, в которых использовался метод эвристической классификации. Этот метод предполагает, что большая часть знаний представлена в виде эвристических правил, связывающих абстрактные категории данных (типичные симптомы) с абстрактными категориями решений (типичные неисправности). Такая форма представления знаний иногда называется "поверхностной", поскольку знания не содержат информации о причинных связях между симптомами и неисправностями (теорию функционирования диагностируемого объекта — машины или живого организма), а отражают только эмпирический опыт. Информация о причинно-следственных связях, определяющих поведение и свойства диагностируемого объекта, принято называть "глубинным" знанием.

Диагностирование, основанное на моделях анализируемых объектов, использует не столько эмпирический опыт эксперта, сколько более или менее полную и непротиворечивую теорию корректного поведения этих объектов. Идея состоит в том, чтобы, располагая на входе данными о наблюдаемых отклонениях в поведении, высказать предположение об одном или нескольких возмущениях в описании системы, которые могли бы объяснить эти отклонения.

Очевидные преимущества подхода, при котором сначала принимаются во внимание знания о принципах поведения объекта, а уже затем эмпирические знания, состоят в следующем.

• Располагая информацией о принципах структурной организации объекта и причинно-следственных связях между свойствами его компонентов и наблюдаемыми проявлениями, разработчик программы может значительно сократить трудоемкий процесс извлечения эмпирических знаний эксперта.
  
• Используемый метод анализа причинно-следственных связей не зависит от самого анализируемого объекта, а следовательно, отпадает необходимость в трудоемкой настройке механизма логического вывода для каждого отдельного приложения.
  
• Поскольку требуется знание только о корректном поведении объекта, потенциально метод должен сработать и при диагностировании неисправностей, которые ранее не возникали и незнакомы эксперту-человеку.
  

Прототипом подобного рода диагностических экспертных систем можно считать программу DART [Genesereth, 1984]. Хотя предметной областью, для которой предназначалась эта программа, является анализ цифровых схем, но использованные в ней язык представления знаний и механизм логического вывода более или менее независимы от этой предметной области. Для представления описания конструкции диагностируемого устройства используются формализм исчисления предикатов и форма доказательства теорем, с помощью которых формируются множества "подозрительных" компонентов и тестов, призванных подтвердить или опровергнуть гипотезы о причинах неисправностей. Метод решения проблем, использованный в DART, опирается на три упрощающих допущения.

(1) Предполагается, что связи между компонентами функционируют правильно, и задача состоит в том, чтобы отыскать те компоненты, неисправность которых может объяснить наблюдаемые симптомы неправильной работы устройства.

(2) Отказы не носят случайного во времени характера, т.е. все компоненты в процессе выполнения диагностических тестов работают стабильно (правильно или неправильно — это уже другой вопрос).

(3) В устройстве имеется единственный отказ.

Каждое из этих предположений, конечно же, очень ограничивает возможность практического применения системы, но в работе [De Kleer and Williams, 1987] было показано, что использование систем отслеживания истинности предположений, основанных на анализе допущений, поможет снять третье из перечисленных ограничений. Это было продемонстрировано в программе GDE (General Diagnostic Engine — система диагностирования общего назначения).

В системе диагностирования, допускающей наличие нескольких неисправностей в устройстве, приходится иметь дело с экспоненциальным ростом пространства гипотез. Чтобы преодолеть возникающие при этом сложности, нужно формировать гипотезы в определенном порядке, принимая во внимание их "конструктивность", а затем выполнять такие процедуры тестирования, которые позволят выбрать из набора конкурирующих гипотез наиболее подходящую, проведя при этом минимальное количество дополнительных измерений. Реализуется такой процесс с помощью комбинации методов отслеживания истинности предположений, основанных на анализе допущений, и методов вероятностного логического вывода.

Как было показано ранее в этом же разделе, методы отслеживания истинности предположений, основанные на анализе допущений, имеют дело с решеткой сред — альтернативных состояний модели мира, которые согласуются с некоторой теорией, но используют при этом отличающиеся допущения. В диагностических приложениях такой неявной теорией является описание диагностируемого устройства, а альтернативные состояния модели мира характеризуются различными комбинациями отказавших компонентов устройства. Если устройство состоит из п компонентов, то теоретически может существовать 2" комбинаций отказов компонентов. Решетка вариантов сред является перечислимым множеством присоединений: элемент с наименьшим номером соответствует отсутствию отказов в компонентах, а элемент с наибольшим номером — отказу всех компонентов устройства. Каждая такая среда называется кандидатом, т.е. гипотезой о том, что именно произошло в неисправном устройстве. Вся решетка сред при такой постановке проблемы будет представлять собой пространство кандидатов.

Если устройство работает нормально, то гипотеза, соответствующая кандидату' с наименьшим номером, прекрасно "объясняет" наблюдаемую ситуацию. Если наблюдаются какие-либо отклонения от нормального функционирования устройства, то наблюдаемые проявления можно считать свидетельствами в пользу той или иной гипотезы в пространстве кандидатов. Поскольку объем этого пространства связан с количеством компонентов в анализируемых устройствах экспоненциальной зависимостью, необходимо использовать в нем какой-либо метод эффективного поиска кандидатов.

Ключевым понятием для такого метода должно быть конфликтующее множество — множество таких компонентов, которые в данной ситуации (т.е. при данных симптомах) не могут одновременно быть исправными. Конфликтующее множество, таким образом, это именно то множество допущений, которое в системе отслеживания истинности предположений, основанной на анализе допущений, формирует среды, несовместимые с данными. Их можно определить, формируя дедуктивное замкнутое выражение для среды и данных, а затем выискивая в нем противоречие. Главная цель системы отслеживания истинности предположений состоит при этом в том, чтобы идентифицировать все минимальные конфликтующие множества. После этого можно определить минимальное множество отказавших компонентов, которое объяснит все наблюдаемые проявления ненормальной работы устройства.

В качестве простого примера рассмотрим решетку сред, представленную на рис. 19.6. В этой решетке C1, C2 и СЗ— компоненты анализируемого устройства. Пусть S — множество наблюдаемых проявлений ненормальной работы этого устройства. Предположим, нам известно, что если наблюдается множество проявлений S, то С1 и С2 не могут быть исправными одновременно, а также С1 и СЗ. Тогда можно выделить среды, помеченные на схеме решетки значками 0, С2 и СЗ (они выделены на схеме как несовместные). Каждая из этих сред имеет какое-либо запрещенное сочетание исправных компонентов. Все другие среды являются кандидатами в пространстве гипотез, но очевидно, что минимальные множества среди них — (С1} и {С2, СЗ}.

В системе отслеживания истинности предположений используется несколько стратегий управления обработкой пространства кандидатов, например:

• стратегия, основанная на предоставлении преимущества тем гипотезам, которые поясняются проще всего; поиск решения начинается с минимальных по объему (количеству элементов) конфликтных множеств;
  
• сохранение в системе просмотренной цепочки логического вывода, что позволяет исключить ее повторный просмотр.
  

В системе GDE также используется мера неопределенности, основанная на теоретико-информационном подходе, с помощью которой выясняется, какие измерения следует выполнить в анализируемой системе. Наилучшей полагается такая измерительная процедура, которая минимизирует энтропию (см. об этом в главе 20), т.е. та, которая вносит наибольшее разнообразие в набор значений вероятностей кандидатов. Предполагается, что априорная вероятность отказа отдельных компонентов известна и что отказы компонентов в вероятностном смысле независимы. Эти же вероятности используются при определении порядка формирования гипотез-кандидатов.

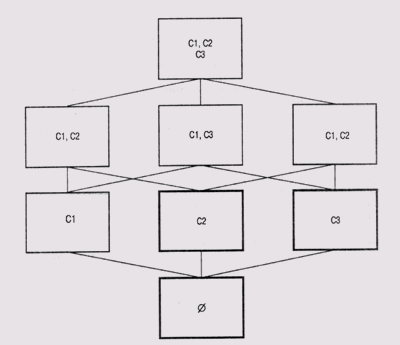
Рис. 19.6. Решетка сред, представляющая пространство кандидатов. Несовместные контексты выделены утолщенным контуром, а минимальные кандидаты заштрихованы