


 |
 |
 |
8.3.2.
Поиск доказательства в системе резолюций
Резолюция
представляет собой правило вывода, с помощью которого можно вывести новую ППФ
(правильно построенную формулу) из старой. Однако в приведенном выше описании
логической системы ничего не говорилось о том, как выполнить доказательство.
В этом разделе мы обратим основное внимание на стратегические аспекты доказательства
теорем.
Пусть р
представляет утверждение "Сократ — это человек", a q —
утверждение "Сократ смертен". Пусть наша теория имеет вид
Т={{¬р,q},
{р}}.
Таким образом,
утверждается, что если Сократ человек, то Сократ смертен, и что Сократ — человек.
{17} выводится из теории Т за один шаг резолюции, эквивалентной правилу
modus ponens. .
Выражения {¬р, q} и {р} "сталкиваются" на паре дополняющих литералов р и ¬р, а {q} является резольвентой. Таким образом, теория Алогически подразумевает д, что записывается в форме Т|-q. Теперь можно добавить новую фразу {q} — резольвенту — в теорию Т и получить таким образом теорию
Т'=
{{ ¬ip, q},
{p}, {q}}.
Конечно, в
большинстве случаев для доказательства требуется множество шагов. Положим, например,
что теория Т имеет вид
В этой теории
р и q сохраняют прежний смысл, а г представляет утверждение
"Сократ — бог". Для того чтобы показать, что Т|- ¬r , потребуются
два шага резолюции:
{¬q,p},{Р}/{q}
{¬q,-r},{q}
/ {-r}
Обратите внимание,
что на первом шаге используются две фразы из исходного множества Т, а
на втором— резольвента {q}, добавленная к Т. Кроме того, следует отметить,
что доказательство может быть выполнено и по-другому, например:
{¬p,q},{¬q,¬r}/{¬p,¬r},
{¬p,¬r},{p}/{¬r}
При таком
способе доказательства к Т добавляется другая резольвента. В связи со
сказанным возникает ряд проблем.
Та схема логического
вывода, которой мы следовали до сих пор, обычно называется прямой, или
восходящей стратегией. Мы начинаем с того, что нам известно, и строим
логические суждения в направлении к тому, что пытаемся доказать. Один из возможных
способов преодоления сформулированных выше проблем — попытаться действовать
в обратном направлении: от сформулированной целевой формулы к фактам, которые
нужны нам для доказательства истинности этой формулы.
Предположим,
перед нами стоит задача вывести {q} из некоторого множества фраз
Т=
{...,{ ¬p, q},...}.
Создается
впечатление, что это множество нужно преобразовать, отыскивая фразы, включающие
q в качестве литерала, а затем попытаться устранить другие литералы,
если таковые найдутся. Но фраза {q} не "сталкивается" с такой
фразой, как, например, { —р, q}, поскольку пара, состоящая из одинаковых
литералов q, не является взаимно дополняющей.
Если q
является целью, то метод опровержения резолюции реализуется добавлением
негативной формулы цели к множеству Т, а затем нужно показать, что формула
Т' = Т U {¬q}
является несовместной.
Полагая, что множество Т непротиворечиво, приходим к выводу, что Т'
может быть противоречивым вследствие Т |- q.
Рассмотрим
этот вопрос более подробно. Сначала к существующему множеству фраз добавляется
отрицание проверяемой фразы {-q}. Затем предпринимается попытка резольвиро-вать
{-q} с другой фразой в Т. При этом существуют только три возможные ситуации.
Эти оставшиеся
литералы можно рассматривать в качестве подцелей, которые должны быть разрешены,
если требуется достичь главной цели. Описанная стратегия получила название нисходящей
(или обратной) и очень напоминает формулирование подцелей в системе
MYCIN.
В качестве примера положим, что множество Т, как и ранее, имеет вид {{¬p,q},{¬q,¬r},{p}}. Мы пытаемся показать, что Т|- ¬r. Для этого докажем, что фраза {r} является следствием существующего множества Т, для чего добавим к этому множеству отрицание фразы ¬r. Поиск противоречия происходит следующим образом:
[{¬q,¬r},{r}]/{¬q}
[{¬p,q},{¬q}]/{¬q}
[{¬p},{p}]/{}
Этот метод
доказ_ательства теорем получил название "опровержение резолюции",
поскольку, во-первых, он использует правило вывода резолюций, а во-вторых, следует
стратегии "от противного" (стратегии опровержения).
Теперь вернемся
к примеру PROLOG-программы, представленному в листинге 8.1. На рис. 8.1 показано
дерево доказательства утверждения above(a, с). Дерево строится сверху
вниз, и каждая ветвь связывает две "родительские фразы", в которых
содержатся дополняющие литералы, с фразой, которая образуется в результате применения
правила резолюции. Ко всем целям, записанным справа от значка ":-",
неявно применяется отрицание. В левой части дерева представлены формулы целей,
а в правой — фразы, взятые из базы данных.
Корнем дерева
является пустая фраза {}. Это означает, что поиск доказательства был успешным.
Добавление негативной фразы :- above (а, с) к исходному множеству (теории) привело
к противоречию. Таким образом, можно утверждать, что фраза above (а, с) является
логическим следствием из этой теории.
Обратите внимание
на роль операции унификации в этом доказательстве. Цель above (а, с)
унифицируется с головной фразой above(X, Y) с помощью подстановки {Х/а, Y/c},
где выражение Х/а можно интерпретировать как "X получает значение
а". Затем эта подстановка применяется к хвостовой части фразы
on(Z, Y), above(X, Z),
из чего следует формулировка подцелей
on(Z,
с), above(a, Z).
Следующая
подцель on(Z, с) унифицируется с on(b, с) подстановкой {Z/b}. Эта подстановка
затем применяется и к оставшейся подцели, которая таким образом превращается
в above (а, b), и так до тех пор, пока не образуется пустая фраза.
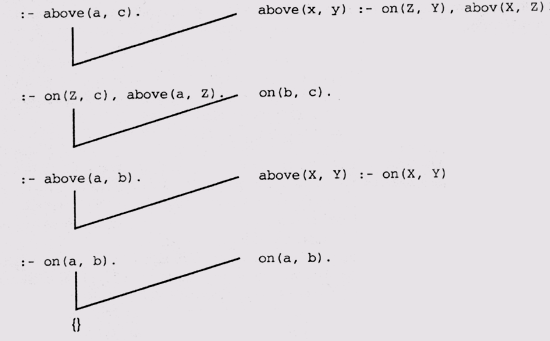
Рис. 8.1.
Дерево доказательства методом опровержения резолюций
Восходящий
процесс доказательства, использующий в качестве отправной точки утверждение,
которое мы стараемся доказать, позволяет сфокусировать внимание на процессе
поиска решения, поскольку анализируемые логические связи по крайней мере потенциально
ведут нас к цели. Правда, основанный на этой стратегии метод опровержения резолюций
не позволяет решить все перечисленные выше проблемы. В частности, этот метод
не гарантирует, что найденный путь доказательства будет короче других (или длиннее).
В следующих
двух разделах мы рассмотрим эволюцию процедурных дедуктивных систем, т.е.
систем, в которых процедуры используются для добавления дополнительных управляющих
свойств в процесс целенаправленного поиска и для представления знаний, которые
не имеют четко выраженного декларативного характера.
Процесс становления этого класса систем весьма поучителен, поскольку демонстрирует, как, отталкиваясь от стандартной логики и добавляя методики, обычно используемые при доказательстве теорем, можно построить успешно функционирующую автоматическую систему доказательства.
 |
 |
 |