

 |
 |
Упражнения
1. Прочитайте
статью Хейеса в сборнике [Brachman and Levesque, 1985]. Как вы думаете,
можно ли считать фреймы не более чем средством реализации подмножества логики
предикатов, или они позволяют смоделировать экстралогические свойства, присущие
человеку, формулирующему суждения?
2. Неоднозначность,
которую мы обнаружили в "проблеме Никсона", можно распространить каскадно
и получить еще более замысловатые примеры. Один из них взят из работы [Touretzky
et al., 1987] (рис. 6.10). Познакомьтесь с этой работой, а затем ответьте
на следующие вопросы.
I) К какому
заключению придет доверчивый резонер, рассуждая об отношении квакера-ре спубликанца
к армии?
II) К какому
заключению придет резонер-скептик?
3. Примеры
сетей с наследованием, представленные на рис. 6.11 и 6.12, также взяты из работы
[Touretzky et a/., 1987]. На этих рисунках представлены две топологически
идентичные
сети, которые отличаются только маркировкой узлов. На рис. 6.11 показано, что
королевские слоны являются исключениями, поскольку не имеют серой окраски, а
на рис. 6.12 показано, что капелланы являются исключениями, поскольку это мужчины,
не склонные к употреблению пива.
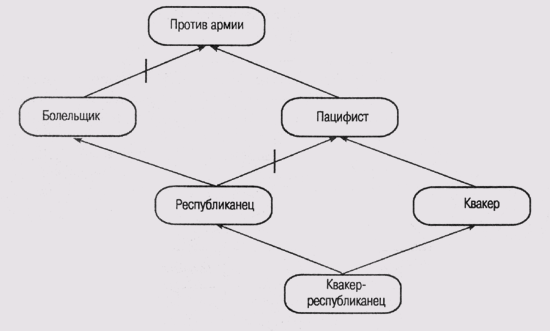
Рис. 6.10.
Сеть с наследованием, в которой имеется каскад неоднозачностей
I) Резонер
Турецкого должен был бы заключить, что в обоих случаях возможно несколько интерпретаций.
Согласны ли вы с таким заключением или нет и по какой причине?
II) Сандуол
полагает, что корректная интерпретация сети на рис. 6.11 состоит в том, что
прямой путь от узла королевский слон к узлу серые животные должен иметь более
высокий приоритет, чем непрямой путь через узел слон [Sandewall, 1986]. А
что вам подсказывает ваша интуиция?
III) Днализируя
сеть, представленную на рис. 6.12, Турецкий пришел к заключению, что изменение
маркировки узлов сети с одной и той же топологией меняет и наше интуитивное
предположение о распространении наследуемых свойств. Заключение о том, что корабельный
капеллан не является любителем пива (как на том настаивает Сандуол), является
менее обоснованным, чем в случае со слонами. В пользу такого заключения Турецкий
приводит следующие аргументы.
С какой из
участвующих в споре сторон согласны вы? Или, возможно, у вас есть аргументы
в пользу обеих точек зрения?
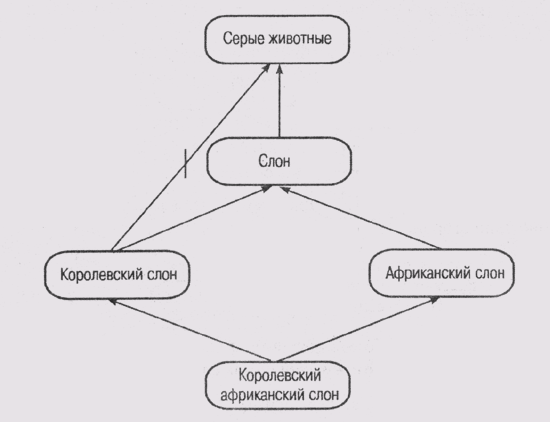
Рис. 6.11.
Проблема "королевского слона"

Рис. 6.12.
Проблема "корабельного капеллана "
4. Просмотрите
пример из врезки 6.1. Придумайте обработчик сообщения для класса square, который
будет вычислять площадь объекта этого класса, например объекта square-one, а
затем присваивать вычисленное значение слоту этого объекта.
Для этого
вам понадобится сначала внести изменения в определение класса square.
(defclass
square (is-a rectangle)
(slot length-of-sides (create-accessor write))
(slot
area (create-accessor write)))
Согласно этому
определению, класс square имеет два слота: length-of-sides — для хранения длин
сторон объекта, area — для хранения его площади. Фацет create-accessor в определении
слота говорит о том, что функции доступа к слоту должны автоматически формироваться
средствами языка CLIPS. Последние самостоятельно сформируют объявления функций
put-length-of-sides и put-area. Эти наименования функций можно затем использовать
в обработчиках сообщений.
Второй шаг
— модифицировать спецификацию объекта, в которую следует включить задание длин
сторон:
(definstances geometry (square-one of square
(length-of-sides
10)))
Теперь остается
только разработать обработчик события, который будет использовать функцию для
установки нужного значения в слот area объекта square-one.
5. Метод, который был реализован в предыдущем упражнении, хорош для работы с квадратами, но с его помощью нельзя решить аналогичную проблему при работе с другими четырехугольниками, представленными в нашей иерархии,— прямоугольниками, параллелограммами и трапециями. Теперь, когда вы знаете, как сформировать слоты и обработчики событий, пользуясь средствами языка CLIPS, попытайтесь решить и эту проблему. Для этого вам потребуется передавать объекту любого класса, расположенного в иерархии ниже узла четырехугольник, сообщение, в ответ на которое соответствующий обработчик должен извлечь данные из слотов, представляющих отдельные исходные параметры формы фигуры (длины сторон, высота и т.д.), и обрабатывать их по формуле, специфичной для фигур каждого вида. Постарайтесь найти такое решение, которое позволяло "бы обрабатывать различные фигуры по возможности единообразно. Учтите, что подклассы могут наследовать и слоты, и обработчики сообщений от своих суперклассов (предшественников).
 |
 |