3.3.2. База знаний системы MYCIN

База знаний системы MYCIN организована в виде множества правил в форме если условие₁ и... и условие_т удовлетворяются то прийти к заключению₁ и... и к заключению n

Эти правила преобразованы в операторы языка LISP (подробнее о программировании базы знаний рассказано в главе 4).

Вот как выглядит перевод на обычный язык типичного правила MYCIN:

ЕСЛИ 1) организм обладает грамотрицательной окраской, и

2) организм имеет форму палочки, и

3) организм аэробный,

ТО есть основания предполагать (0,8), что этот микроорганизм относится к классу enterobacteriaceae.

Такого рода правила названы оргправилами (ORGRULES) и в них сконцентрированы знания о таких организмах, как strepococcus , pseudonomas и enterobacteriaceae.

Это правило говорит о том, что если организм имеет форму палочки, пятнистую окраску и активно развивается в среде, насыщенной кислородом, то с большой вероятностью его можно отнести в классу enterobacteriaceae. Число 0.8 называется уровнем соответствия (tally) правила, т.е. мерой правдоподобия заключения, сделанного на основании сформулированных условий. Методика использования уровня соответствия правила будет рассмотрена ниже. Каждое правило такого вида можно рассматривать как представление в машинной форме некоторого элемента знаний эксперта. Возможность применить правило определяется тем, удовлетворяются ли в конкретной ситуации условия, сформулированные в первой его части. Сформулированные условия также носят нечеткий характер и могут удовлетворяться с разной степенью истинности. Поэтому в результате импортирования правил из базы знаний применительно к конкретной ситуации формируется более общее правило, включающее и оценки уровня истинности соблюдения условий:

если условие1 удовлетворяется с истинностью х₁ и ... и условие_m удовлетворяется с истинностью х_м,

то прийти к заключению₁ со степенью уверенности у₁ и ... и к заключению_n со степенью уверенности у_n.

Здесь степень уверенности, связанная с каждым заключением, является функцией от оценок истинности соблюдения условий и уровня соответствия, отражающего степень уверенности эксперта при формулировке первичных оргправил.

Фактически правило является парой "предпосылка—действие"; такое правило иногда традиционно называют "продукцией" (подробнее об этом см. в главе 5). Предпосылка — это совокупность условий, а уверенность в достоверности предпосылки зависит от того, насколько достоверной является оценка условий. Условия — это предположения о наличии некоторых свойств, которые принимают значения истина либо

ложь с определенной степенью достоверности. Примером может служить условие в приведенном выше правиле:

"Организм имеет форму палочки".

Действие — это либо заключение, либо рекомендация о том, какое действие предпринять. Примером заключения может служить вывод о том, что данный организм относится к определенному классу. Пример рекомендации — сформулированный перечень лечебных процедур.

Мы детально проанализируем процесс применения правил в последующих разделах. А сейчас кратко остановимся на том, как в MYCIN для представления знаний используются структуры другого вида.

Помимо правил, в базе знаний MYCIN также хранятся факты и определения. Для их хранения используются разные структурные формы:

• простые списки, например списки всех микроорганизмов, известных системе;
  
• таблицы знаний с записями об определенных клинических показаниях и значениях, которые эти показания имеют при разных условиях; примером может служить информация о форме микроорганизмов, известных системе;
  
• система классификации клинических параметров соответственно контексту, в котором эти параметры рассматриваются, например являются ли они свойством (атрибутом) пациентов или микроорганизмов.
  

Значительная часть знаний хранится не в виде правил, а в виде свойств, ассоциированных с 65 клиническими параметрами, известными системе MYCIN. Например, форма— это атрибут микроорганизма, который может принимать самые разнообразные значения, например "палочка" или "кокон". Система также присваивает значения параметрам и для собственных нужд — либо для упрощения мониторинга взаимодействия с пользователем, либо для индексации при определении порядка применения правил.

Информация о пациенте хранится в структуре, названной контекстным деревом (context tree). На рис. 3.3 показано контекстное дерево пациента ПАЦИЕНТ 1. В это дерево включены три культуры организмов (например, полученные из анализа крови пациента) и текущие назначения, которые нужно учитывать при анализе, поскольку они сопряжены с приемом определенных лекарственных средств. С культурами связаны микроорганизмы, присутствие которых предполагается на основании данных, полученных в лаборатории, а с микроорганизмами — лекарственные средства, оказывающие воздействие на них.

Предположим, что в записи, связанной с узлом ОРГАНИЗМ-1 в этой структуре, хранятся данные

ГРАН = (ГРАМ-ОТР 1.0)

МОРФ = (ПАЛОЧКА .8) (КОКОН .2)

ВОЗДУХ = (АЭРОБ .6),

которые имеют следующий смысл:

• совершенно определенно организм имеет грамотрицательную окраску;
  
• со степенью уверенности 0.8 организм имеет форму палочки, а со степенью уверенности 0.2 — форму колбочки;
  
• со степенью уверенности 0.6 ОРГАНИЗМ-1 является аэробным (т.е. воздушная среда способствует его росту).
  

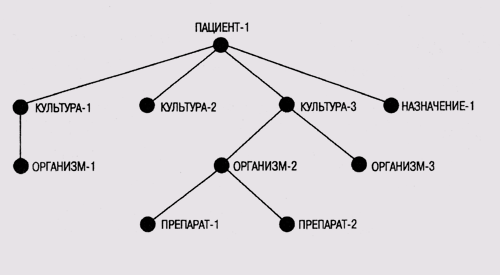
Рис. 3.3. Типичное контекстное дерево в системе MYCIN ([Buchanan and Shortliffe, 1984])

Теперь предположим, что применяется сформулированное выше правило. Нам требуется определить степень уверенности в выполнении всех трех перечисленных в нем условий применительно к данным, представленным в ОРГАНИЗМ-1. Степень уверенности в выполнении первого условия равна 1.0, второго — 0.8, а третьего — 0.6. Степень уверенности в выполнении совокупности условий принимается равной минимальному из значений, характеризирующих отдельные компоненты, т.е. 0.6.

В качестве оценки достоверности совокупности принимается минимальное значение по той причине, что рассчитывать на выполнение всех условий вместе можно не более, чем на выполнение самого "ненадежного" из них. Здесь очень уместна аналогия с цепочкой, прочность которой не может быть выше прочности самого слабого ее звена. Можно рассмотреть и обратный случай: какова степень уверенности в невыполнении совокупности условий? Она равна максимальному из значений, характеризующих невыполнение отдельных компонентов. Сформулированные выше соглашения легли в основу методики формирования неточных суждений, так называемой нечеткой логики, о которой мы поговорим в главе 9.

В данном случае мы приходим к заключению, что микроорганизм, описанный в узле ОРГАНИЗМ-1, относится к классу энтеробактерий со степенью уверенности, равной 0.6 х 0.8 = 0.48. Сомножитель 0.6 — это степень уверенности в выполнении совокупности условий, перечисленных в правиле, а 0.8 — степень уверенности в том, что правило дает правильное заключение, когда все означенные в нем условия гарантированно удовлетворяются. За сомножителями и результатом этого выражения закрепился термин коэффициента уверенности (CF— certainty factor). Таким образом, в общем случае имеем:

СF(действие) = СF(предпосылка) х СРF(правило)

Более подробно о коэффициентах уверенности мы поговорим в главах 9 и 21, где основное внимание уделяется теме представления неопределенности. Коэффициенты уверенности имеют много общего с оценками вероятности, но между этими двумя понятиями есть и определенные различия. Свойства этих коэффициентов не всегда подчиняются правилам теории вероятности и, таким образом, с математической точки зрения вероятностями не являются. Но методы вычисления коэффициентов уверенности некоторой совокупности правил или действий по коэффициентам уверенности, характеризующим отдельные компоненты в этой совокупности, в значительной мере напоминают методы вычисления вероятности сложных событий по вероятностям совершения событий-компонентов.